Educational Codeforces Round 8 F: Bear and Fair Set

問題概要

原文 → Problem - F - Codeforces

の倍数 と、整数 が与えられるので、以下を全て満たす正の整数集合を構築できるかどうか判定せよ。

• 要素数は で、値は全て 以下で相異なる
• の各元 について、要素を で割ったあまりが になるような、集合内の要素の数はちょうど 個である
• 以下の 個の条件を全て満たす
  • 集合内の から までの整数を全て数えた結果が である

解説

まず、各条件を の値でソートします。すると、 はいくつかの区間に分かれることになり、各区間内で数をいくつ選べば良いかもわかります。

以下のようにグラフを作り、最大フローが であるかどうかで判定可能です。

• source に「余りが 」を表す頂点をそれぞれつなげ、その頂点集合を とする。容量はすべて
• sink に、各区間に対応するような頂点をつなげ、その頂点集合を とする。容量はその区間内で選ぶべき個数になる。
• に属する頂点と に属する頂点との間は、対応する区間内にあまりが である要素がいくつあるかに応じて容量を設定してつなげる

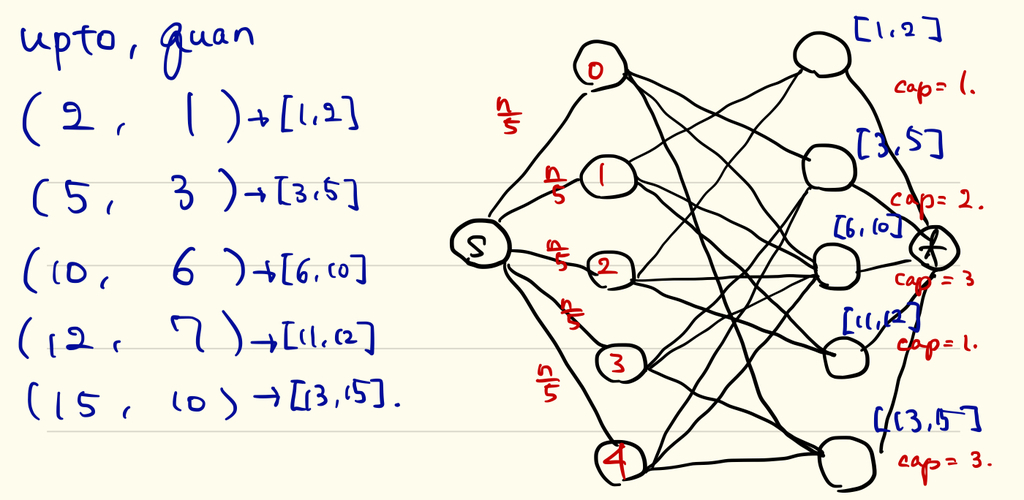
また、Hall の結婚定理を使っても解くことができます。 の頂点部分集合 全てに対して、 と を結ぶ辺として使用される本数の最小値・最大値を求め、これをそれぞれ とします (下限が 0 でないことに注意)。条件を満たすような集合が存在する、つまり適切なマッチングが存在するための必要十分条件は、 になります (詳しくは Hall の結婚定理 を調べてください)。この方針でやると (この問題において ) で解けます。

ソースコード

以下の実装は普通にフローを流す方の解法です。

// フロー略
const int K = 5;
signed main() {
    int N, B, Q; scanf("%lld%lld%lld", &N, &B, &Q);

    vector< tuple<int, int> > queries;
    for(int i=0; i<Q; i++) {
        int upto, quan; scanf("%lld%lld", &upto, &quan);
        queries.emplace_back(upto, quan);
    }
    queries.emplace_back(B, N);
    sort(queries.begin(), queries.end());

    Flow<int> fl(K + queries.size() + 2);
    int source = K + queries.size(), sink = source + 1;

    // source <-> A
    for(int i=0; i<K; i++) {
        fl.add_edge(source, i, N / K);
    }

    bool ok = true;
    int pre_num = 0, pre_quan = 0;
    for(size_t x=0; x<queries.size(); x++) {
        auto q = queries[x];
        int upto, quan; tie(upto, quan) = q;
        if(pre_quan > quan) ok = false;
        int cap = quan - pre_quan;
        
        vector<int> cnt(K);
        for(int i=pre_num+1; i<=upto; i++) {
            int mod = i % K; cnt[mod]++;
        }

        // A <-> B
        for(int i=0; i<K; i++) {
            fl.add_edge(i, K + x, cnt[i]);
        }
        // B <-> sink
        fl.add_edge(K + x, sink, cap);

        pre_num = upto, pre_quan = quan;
    }

    int res = ok ? fl.max_flow(source, sink) : -1;
    printf("%s\n", res == N ? "fair" : "unfair");
    return 0;
}

Hall の結婚定理を用いた解法は公式の実装がわかりやすいです。