Codeforces Round #540 Div.3 F1: Tree Cutting (Easy Version)

問題概要

原文 → Problem - F1 - Codeforces

頂点からなる木が与えられ、各頂点は赤・青のどちらかで塗られているか、何も塗られていないかのいずれかである。

木の辺を 1 つだけ取り除き、同じ連結成分内には色が高々 1 種類まで登場するようにしたい。これを達成できる辺の切り方は何通り存在するか？

解説

辺は 1 つだけしか取り除かないので、DFS をして解くことができます。

まず、適当に根を設定して根付き木として考えます。各頂点 に関して、「 を根とする部分木内に存在する 赤 / 青 の頂点数」を覚えておきます。これは DFS で可能です。

次に、ある辺を切ったときにできる 2 つの連結成分 について、 赤 / 青 がそれぞれいくつ含まれるかを各辺に対して計算します。これは、一方 () は DFS 時に得られた値を使えば良いですし、もう一方 () は全体から の情報を引くことで得られます。

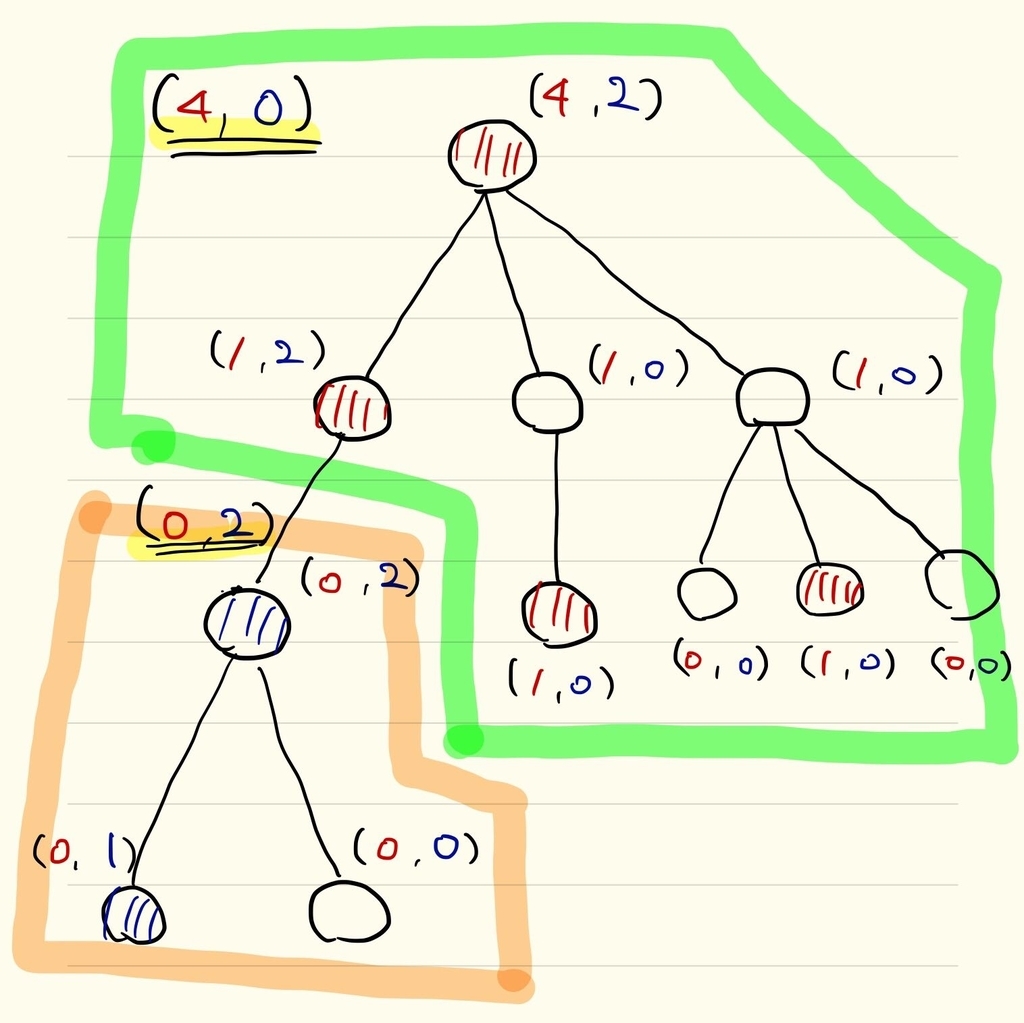
どちらの連結成分に関しても、どちらか一方のみの色が含まれている場合、それは条件を満たす辺のひとつです。

ソースコード

const int S = 300000;
int cntR[S+10], cntB[S+10], col[S+10];
int ans;
vector<int> G[S+10];

void dfs(int cur, int par=-1) {
    if(col[cur] == 1) cntR[cur]++;
    if(col[cur] == 2) cntB[cur]++;
    for(auto to : G[cur]) {
        if(to == par) continue;
        dfs(to, cur);
        cntR[cur] += cntR[to];
        cntB[cur] += cntB[to];
    }
}

void dfs2(int cur, int par=-1, int root=0) {
    for(auto to : G[cur]) {
        if(to == par) continue;
        dfs2(to, cur);
        int R1 = cntR[to], B1 = cntB[to];
        int R2 = cntR[root] - R1, B2 = cntB[root] - B1;

        bool ok = true;
        ok &= (R1 == 0 or B1 == 0);
        ok &= (R2 == 0 or B2 == 0);
        ans += ok;
    }
}

signed main() {
    int N; scanf("%lld", &N);
    for(int i=0; i<N; i++) {
        scanf("%lld", &col[i]);
    }

    for(int i=0; i<N-1; i++) {
        int a, b; scanf("%lld%lld", &a, &b);
        a--; b--;
        G[a].push_back(b);
        G[b].push_back(a);
    }
    dfs(0);
    dfs2(0);

    cout << ans << endl;
    return 0;
}