9/14〜9/16 に HUPC2020 が開催され、9/14 は 北大セット でした。元々は RUPC2020 の北大セットとして出す予定だったので自分もまだ作問に携わっていて、今回で大学合宿の作問は卒業ということになりました。思い返してみれば、RUPC2017 からセット提供するごとに毎回作問しているのでなんだかんだ 3 年半くらい関わったことになります (しかも HUPC 主催で作問機会を自ら増やしているという・・・)。そう考えるとなんとなく結構やったのかもという気持ちになりますね。
今回もセットを作るにあたって相当いろいろやったので、振り返ってみます (なんかこういうのやりたくなっちゃうんですよね、半分ポエムだけど許してください)
続きを読むこの辺の (海外の ICPC 問題の) 記事書く人いなさそうなので書きます
整数 が与えられる。
を満たす整数の組
であって
が互いに素であるものの個数を求めよ。
※ 計算量を書くために、 としています。
お察しの通り を書いても落ちると思います。それよりも時間計算量が良いものを書く必要があります。
を、「
を満たす組
であって
が互いに素であるものの個数」とします。元の問題で要求されていることとは微妙に異なりますが、この関数を組み合わせることで元の問題を表現することができます。具体的には
を考えれば良いです (二次元累積和を実装したことがあるならば、それがイメージの助けになるかと思います)
では、この関数 はどのようにすれば高速に計算できるでしょうか？整数の組
の
以外で最小の公約数が
であるとして、包除原理のように考えると以下のようになります。
ここで「引く」「足す」「考慮しない」など、それぞれの場合の数に対して といった係数がかかることになりますが、この係数はまさにメビウス関数 (Mobius function) そのものです。この関数について詳しく知りたい方は メビウスの反転公式の証明と応用 | 高校数学の美しい物語 を見てください。メビウス関数はエラトステネスのふるいを動かす際に一緒に計算できるので、元の問題は
で解けます。
const int MAXN = 10000010; int mu[MAXN + 5]; bool is_prime[MAXN + 5]; int main() { fill(is_prime + 2, is_prime + MAXN + 1, true); fill(mu, mu + MAXN + 1, 1); for(int i=2; i<=MAXN; i++) { if(!is_prime[i]) continue; mu[i] = -1; for(int k=i<<1; k<=MAXN; k+=i) { is_prime[k] = false; if((k/i) % i == 0) mu[k] = 0; else mu[k] = -mu[k/i]; } } int A, B, C, D; scanf("%d%d%d%d", &A, &B, &C, &D); auto calc = [&](int x, int y) { ll res = 0; for(int i=1; i<=min(x, y); i++) { res += 1LL * (x/i) * (y/i) * mu[i]; } return res; }; ll ans = calc(B, D) - calc(A-1, D) - calc(B, C-1) + calc(A-1, C-1); printf("%lld\n", ans); return 0; }
原文はこちら
棒が 本ある。これらのうち異なる
本に輪を投げ入れることを
回行う。投げ入れ方によって以下のように得点が定められる。
得られる得点を最大化せよ。最大化した得点が負になることもある。
制約
おそらくどう考えても動的計画法のアプローチでは無理だと思います。他のアプローチを考えましょう。満たすべき制約がそれなりに多いので、フローを考えてみることにします。必要そうな頂点や辺を順に考えていきます。
符号を反転させて最小化問題として捉え、最小費用流で考えてみると、途中までは以下のようにグラフを作ると良くなります。辺に書いてある とは、流量が
でコストが
であることを表します。
※図における はすべて
に置き換えて読んでください
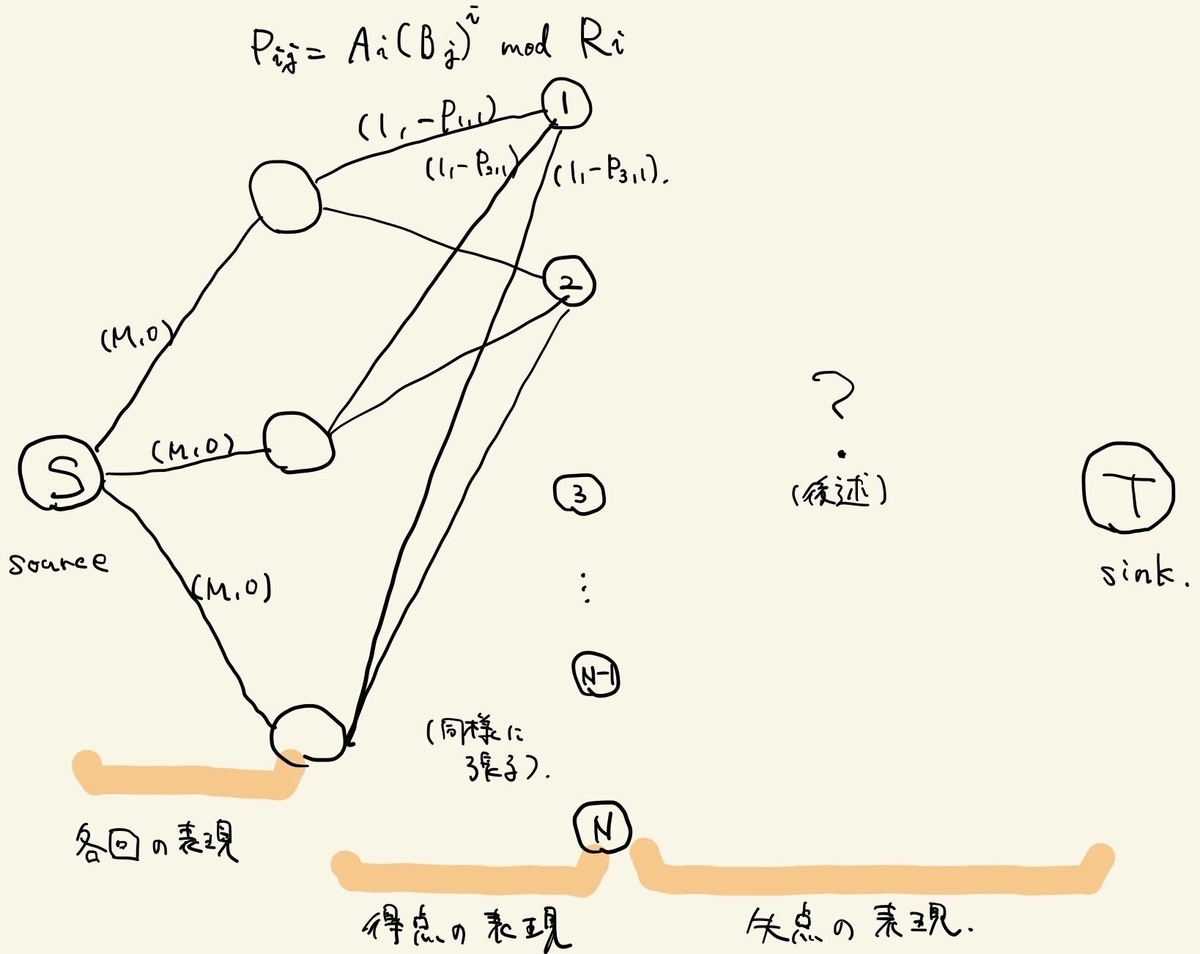
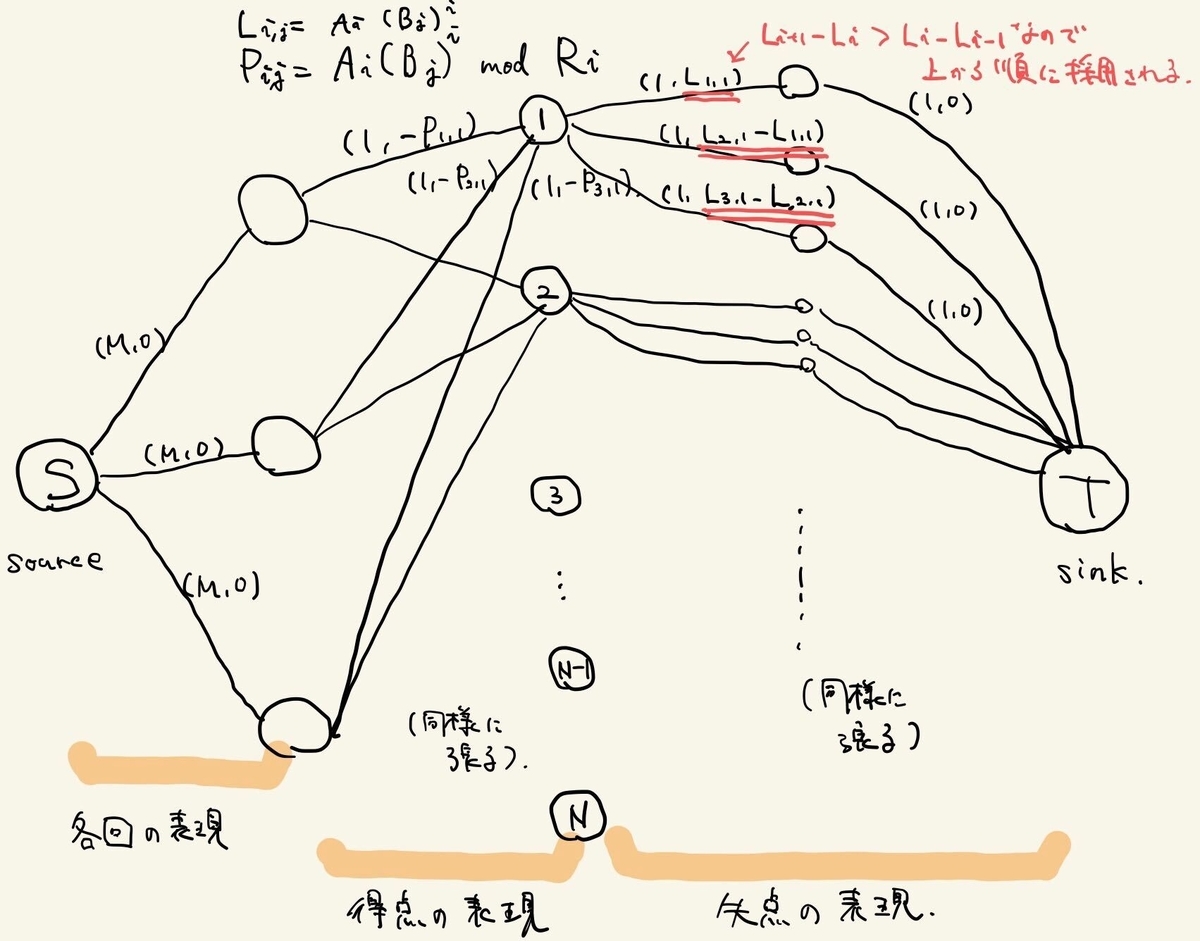
さて、実際には失点を表現できるようにグラフを作らなければならないですが、後半のグラフはどう作ればよいでしょうか？ここで超重要なのが、 であるので 失点は指数的に増える ということです。より具体的に言うと、
ならば
であることが重要です。
の差分がどんどん広がっていくわけですので、以下のように辺を張ると、上の頂点から貪欲にいくつか使用したもののみが最小費用流の解となりえることがわかるので、このように張ると良いです。
// フロー 略 int main() { int N, M; cin >> N >> M; vector<ll> A(N), B(N); for(int i=0; i<N; i++) cin >> A[i]; for(int i=0; i<N; i++) cin >> B[i]; vector<ll> R(3); for(int i=0; i<3; i++) cin >> R[i]; Flow<ll, ll> fl(2 + 3 + N + 3*N, LONGINF, LONGINF, LONGINF); int source = 3 + N + 3*N, sink = source + 1; for(int i=0; i<3; i++) { fl.add_edge(source, i, M, 0); } for(int r=0; r<3; r++) { for(int i=0; i<N; i++) { ll val = A[i]; for(int j=0; j<=r; j++) (val *= B[i]) %= R[r]; fl.add_edge(r, 3+i, 1, -val); } } for(int i=0; i<N; i++) { ll acc = 0; for(int r=0; r<3; r++) { ll val = A[i]; for(int j=0; j<=r; j++) (val *= B[i]); fl.add_edge(3+i, 3+N+(3*i+r), 1, val - acc); acc += val - acc; } } for(int i=0; i<N; i++) { for(int r=0; r<3; r++) { fl.add_edge(3+N+(3*i+r), sink, 1, 0); } } ll ans = fl.mincost_flow(source, sink, 3*M); assert(ans != LONGINF); printf("%lld\n", -ans); return 0; }
検定の問題としては要求知識がコアだな・・・と少し思いましたが、過去問の傾向見るとこんなもんかなという気もしますね。
